student's night out problem solved with LINDO
Rigid Model
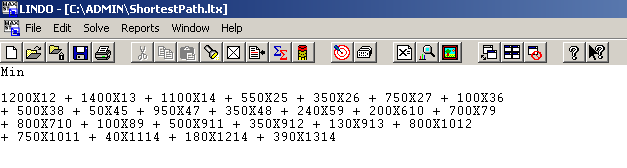
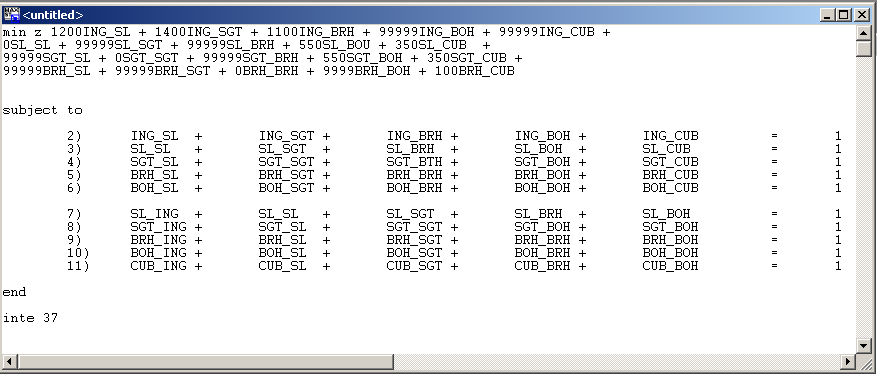
When using LINDO to solve the shortest path problem as a Transhipment Problem an objective function as well as constraints need to be set up and entered into the program. A general formula was obtained which can be used to set up the required objective function and constraints. In the network there are m nodes and n arcs and the cost (in our case distance) associated with each arc is Cij (moving from I to j). The aim is therefore to find the shortest path (least cost) from node 1 to m.
Objective function: Different distances are associated with the various paths between the nodes. The paths total distance is calculated as the sum of the distances of all the arcs on the path. Binary variables are then defined as Xij. If the arc I to j is on the shortest path Xij = 1, if not Xij is set to 0. The path starts with the origin node, ending with the destination node.
Min
∑ CijXij (all the arcs)
Objective function: Different distances are associated with the various paths between the nodes. The paths total distance is calculated as the sum of the distances of all the arcs on the path. Binary variables are then defined as Xij. If the arc I to j is on the shortest path Xij = 1, if not Xij is set to 0. The path starts with the origin node, ending with the destination node.
Min
∑ CijXij (all the arcs)
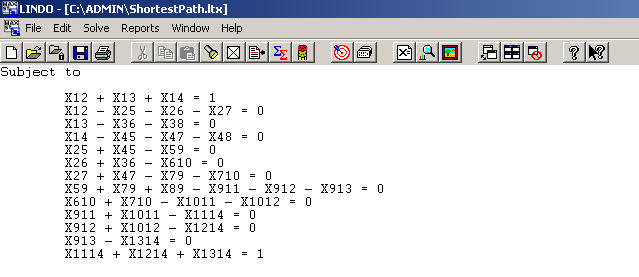
Constraints: The constraints are broken into three groups: Origin, Intermediate and Destination node constraints. The Origin Node constraint is defined by the fact that one has to leave the Origin and go to a possible neighboring node. The Intermediate Node constraints are defined by the fact that when the path enters a node it must leave that node. Finally the destination node refers to the fact that the final node must be reached from one of its neighboring nodes.
∑ Xij - ∑ Xij = 1 Origin Node i (arcs out) (arcs out)
∑ Xij - ∑ Xij = 0 Intermediate Node (arcs out) (arcs out)
∑ Xij - ∑ Xij = 1 Destination Node (arcs out) (arcs out)
∑ Xij > 0
∑ Xij - ∑ Xij = 1 Origin Node i (arcs out) (arcs out)
∑ Xij - ∑ Xij = 0 Intermediate Node (arcs out) (arcs out)
∑ Xij - ∑ Xij = 1 Destination Node (arcs out) (arcs out)
∑ Xij > 0
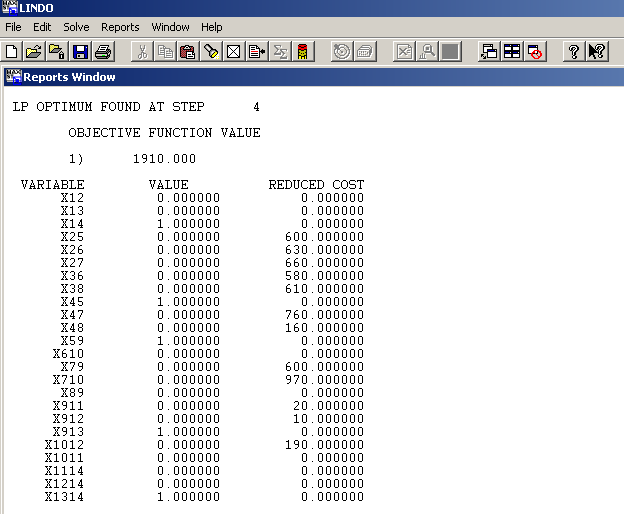
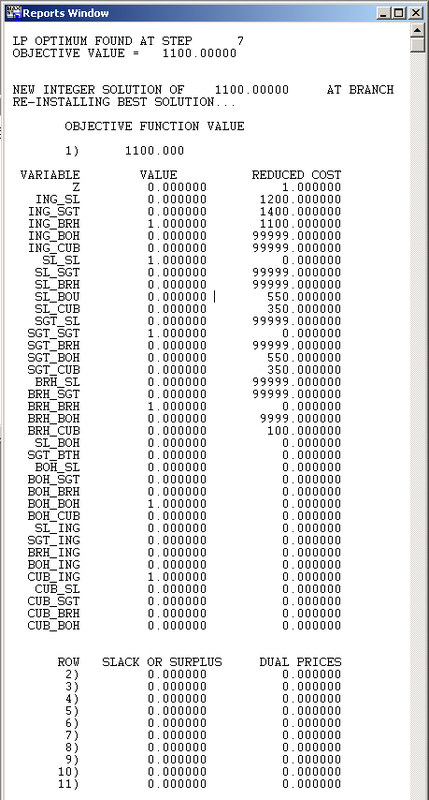
The LINDO output is shown below
LINDO calculated that the shortest path from the Engineering Faculty to Springboks is 1910m
The Exact route is shown in the VALUE column where the binary variables are equal to 1
The Exact route is shown in the VALUE column where the binary variables are equal to 1
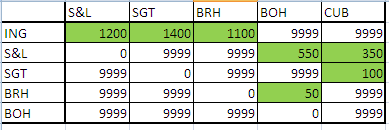
Flexible model (Transportation problem)
Lindo can only hanlde 50 integer variables. The student's night out problem was reduced to the following:
The objective function will be to minimize the total distance between Engineering and Cubana.
The following input and output was given: